One question frequently arises among investors considering bond strategies: Is this the time to invest in fixed income? Like any market, timing interest rates is challenging. This note will not address the merits (or potential) of timing the interest rate market. Rather, it addresses one key, and often overlooked, aspect of interest rate levels – specifically, rate changes that are currently priced into the market. An understanding of the implications of this market pricing, as embedded in the break-even yield curve, is necessary to make well-informed decisions regarding the interest rate market.
Explanation of Break-Even Rates
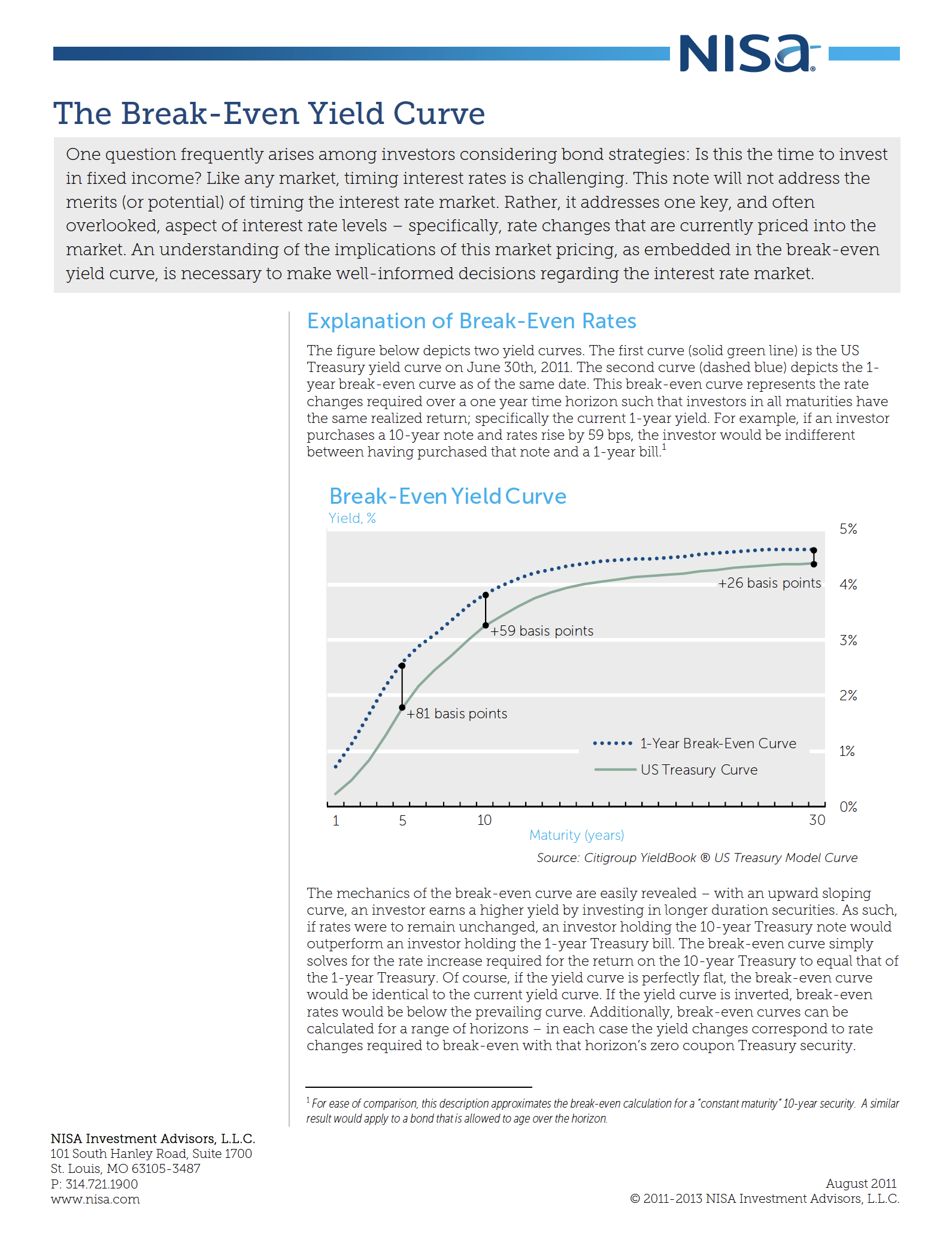
The figure below depicts two yield curves. The first curve (solid green line) is the US Treasury yield curve on June 30th, 2011. The second curve (dashed blue) depicts the 1-year break-even curve as of the same date. This break-even curve represents the rate changes required over a one year time horizon such that investors in all maturities have the same realized return; specifically the current 1-year yield. For example, if an investor purchases a 10-year note and rates rise by 59 bps, the investor would be indifferent between having purchased that note and a 1-year bill.1
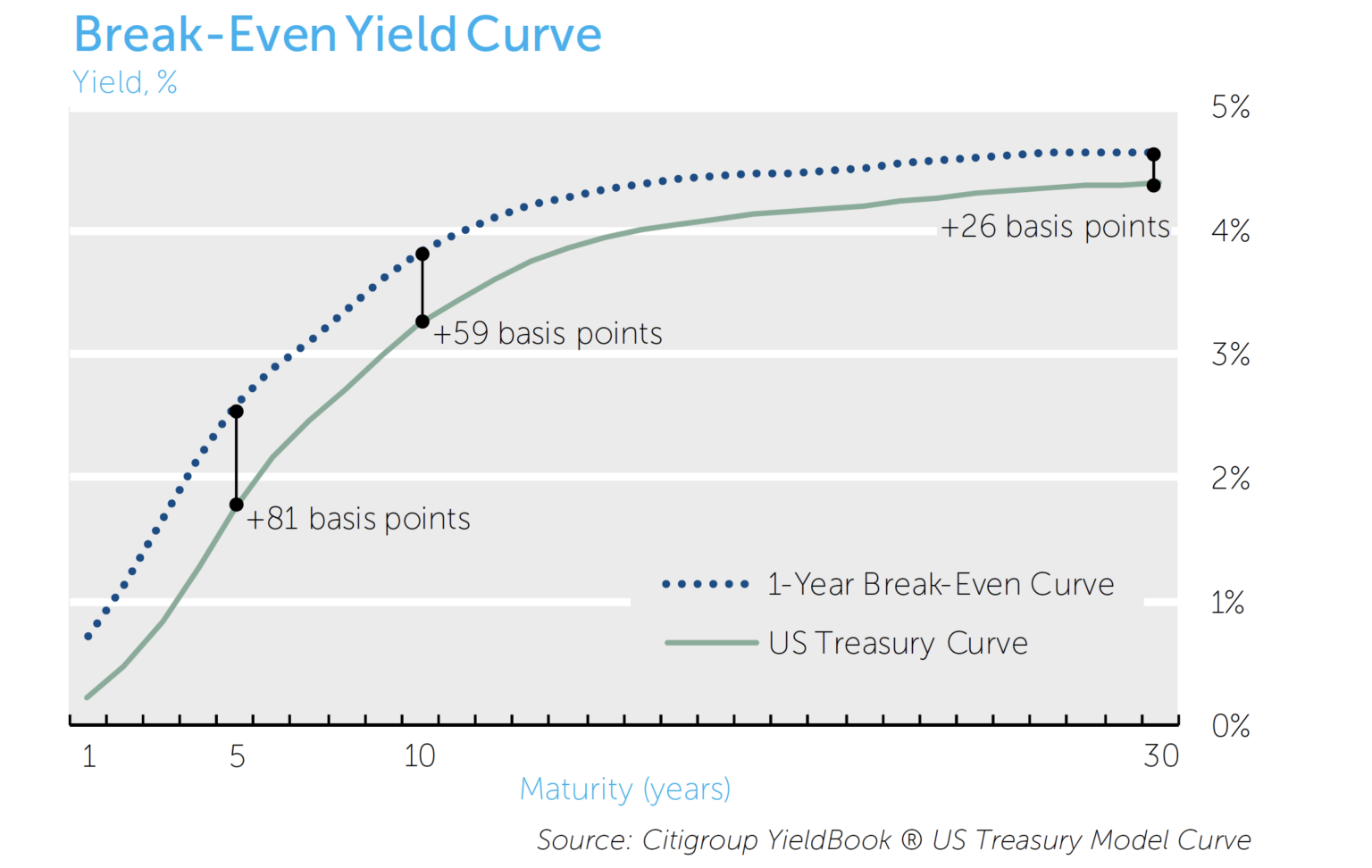
The mechanics of the break-even curve are easily revealed – with an upward sloping curve, an investor earns a higher yield by investing in longer duration securities. As such, if rates were to remain unchanged, an investor holding the 10-year Treasury note would outperform an investor holding the 1-year Treasury bill. The break-even curve simply solves for the rate increase required for the return on the 10-year Treasury to equal that of the 1-year Treasury. Of course, if the yield curve is perfectly flat, the break-even curve would be identical to the current yield curve. If the yield curve is inverted, break-even rates would be below the prevailing curve. Additionally, break-even curves can be calculated for a range of horizons – in each case the yield changes correspond to rate changes required to break-even with that horizon’s zero coupon Treasury security.
The importance of the break-even curve for investors considering tactical interest rate investing is that it provides a framework for implementing interest rate views. For an investor to profit from a bearish view on bonds over a given time horizon, the investor must expect rates to rise more than the break-even level over that period. For an investor to profit from a bullish view on bonds, the investor must expect rates to rise less than the horizon break-even level.2
Break-even Curves, Forward Curves, and Expectations
The break-even curve is often referred to as the forward curve because the rates embedded in it are used to set forward pricing, such as for derivative instruments. While mathematically identical, we prefer the more descriptive “break-even” term to avoid ambiguity. The break-even rates illustrate the context of rate changes an investor must have in mind to have an informed view on interest rates. With this in mind, there is no need to believe that forward rates/break-even rates are good predictors of future rates for them to be useful. They are, in fact, always helpful in comparing the relative performance of different interest rate strategies.
Because there is no reason to assume the break-even curve represents the market’s expectations of future rates, it follows that the market can have expectations different from those embedded in the break-even curve, thus offering return premiums for different investors. For example, if there are positive term premiums, the market must expect rates to rise by less than what is priced into the break-even curve. If rates do in fact rise by this lesser amount, the investor will retain some portion of the higher yield associated with the longer bond, thus earning a term premium.
Like other risk premiums (e.g., equity risk premiums), term premiums are unobservable, thus making true market expectations unobservable. So while investors with opinions can never be certain about the market’s expectations for rates, the simplicity of the breakeven curve allows them to know with certainty what rate moves are required to benefit from their views.
Conclusion
The break-even yield curve provides investors a useful tool to determine rate changes currently priced into the market. Analysis of this curve is necessary for investors to make fully informed decisions regarding their interest rate investment strategies and incorporate tactical views into these strategies accordingly.